I. Overview
After obtaining a 256-bit private key, the public key is calculated from the private key using the elliptic curve cryptography algorithm in a finite field. The basic mathematical knowledge involved belongs to the field of number theory, including modular arithmetic, prime number concepts, Euler's function, Euler's theorem, Euclidean extended theorem, RSA encryption theory, elliptic curve point operations, in other words, it can be understood as an upgraded version of RSA cryptography.
II. Elliptic Curve Cryptography (ECC)
Elliptic curve encryption is unidirectional, also known as asymmetric encryption. Its core idea is that the operation is irreversible, or that as long as an operation method has irreversible characteristics, it can be used as asymmetric encryption. 'Modular arithmetic' and 'point operations' are currently popular irreversible operations or unidirectional functions, or unidirectional operations.
1. Elliptic Curve Function (Real Number Domain)
The most commonly used class of elliptic curve functions is the Weierstrass standard form, which has different representations in different fields. The form commonly used in cryptography is: y^2=x^3+ax+b (x, y belong to real numbers)
In the Bitcoin system, a specific elliptic curve function (SEC, Standards for Efficient Cryptography) is used: y^2=x^3+7 (a=0, b=7, x, y belong to real numbers), its coordinate graph is as follows.

Figure 1, the function graph of y^2=x^3+7 (x, y belong to real numbers)
Superficially, the 'elliptic curve function' seems unrelated to 'elliptic functions', but why is it called elliptic? This is because in early integral research, attempts were made to calculate the arc length of an elliptic geometric figure, which eventually developed into a deeper function theory, hence the name 'elliptic curve function'.
2. 'Point Operations' of the Elliptic Curve Function (Real Number Domain)
Point operations are a relatively special type of operation. We ordinary people do not need to study them too deeply; this is something that students engaged in mathematics-related professional fields need to consider. We just need to know its basic principles and rules.
In point operations, we first need to understand 'point addition', then understand 'point multiplication', and then we will know why the formula for calculating the public key in Bitcoin is K=k*G (K is the public key, k is the private key, G is the base point).
A. Point Addition

Figure 2, 'Point Addition' diagram. Assuming there are two points P and Q on the elliptic curve, then the result of the point operation P+Q is: connecting points P and Q into a straight line, the straight line intersects the curve at a third point -R, finding the symmetric point R of -R relative to the X-axis, then this point is the result of P+Q, that is, P+Q=R.
B. Point Multiplication
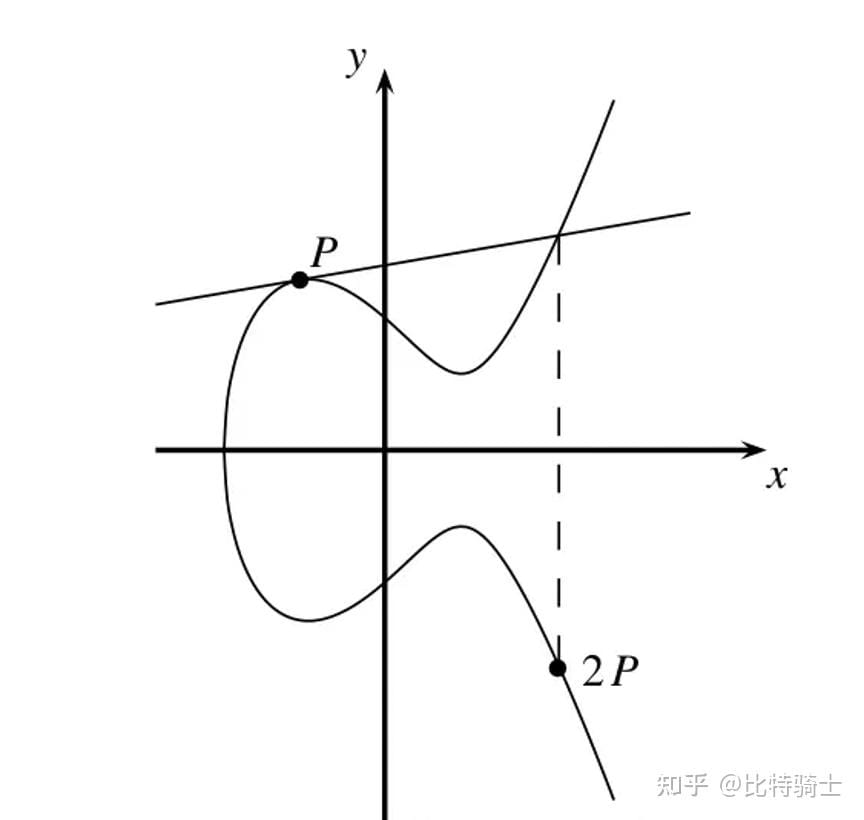
Figure 3, 'Point Multiplication' diagram. Assuming P and Q overlap, then point addition P+Q=2P, which is point multiplication 2*P. On the graph, it is equivalent to drawing the tangent at point P that intersects the curve at a third point -R, and finding the x-axis symmetric point of -R, then this point is the result R of 2*P, that is, 2P=R. Similarly, if we draw a tangent through point R (i.e., the point 2P), we can find the point 2*2P=4P.
Homework: Combine with point addition operation, try to find where the point 3P should be?